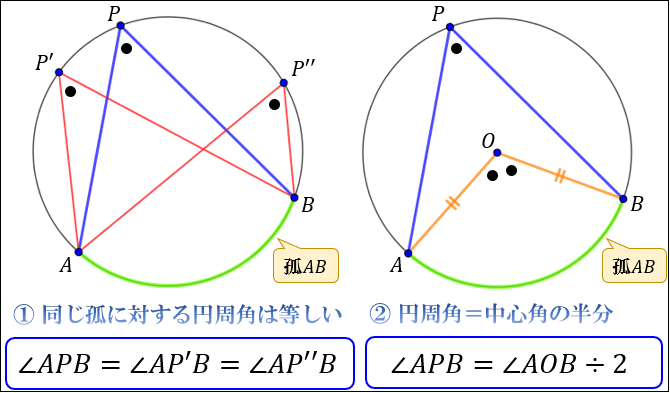
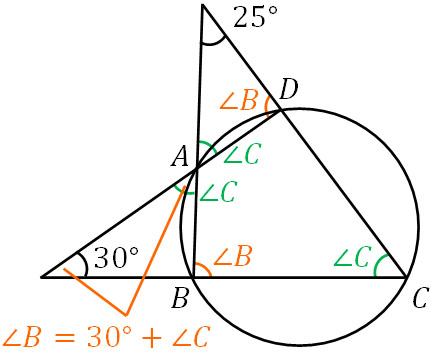
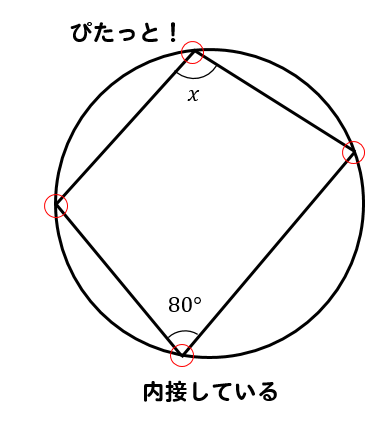
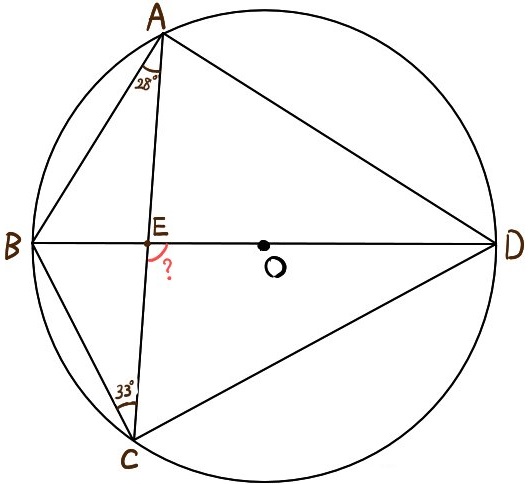
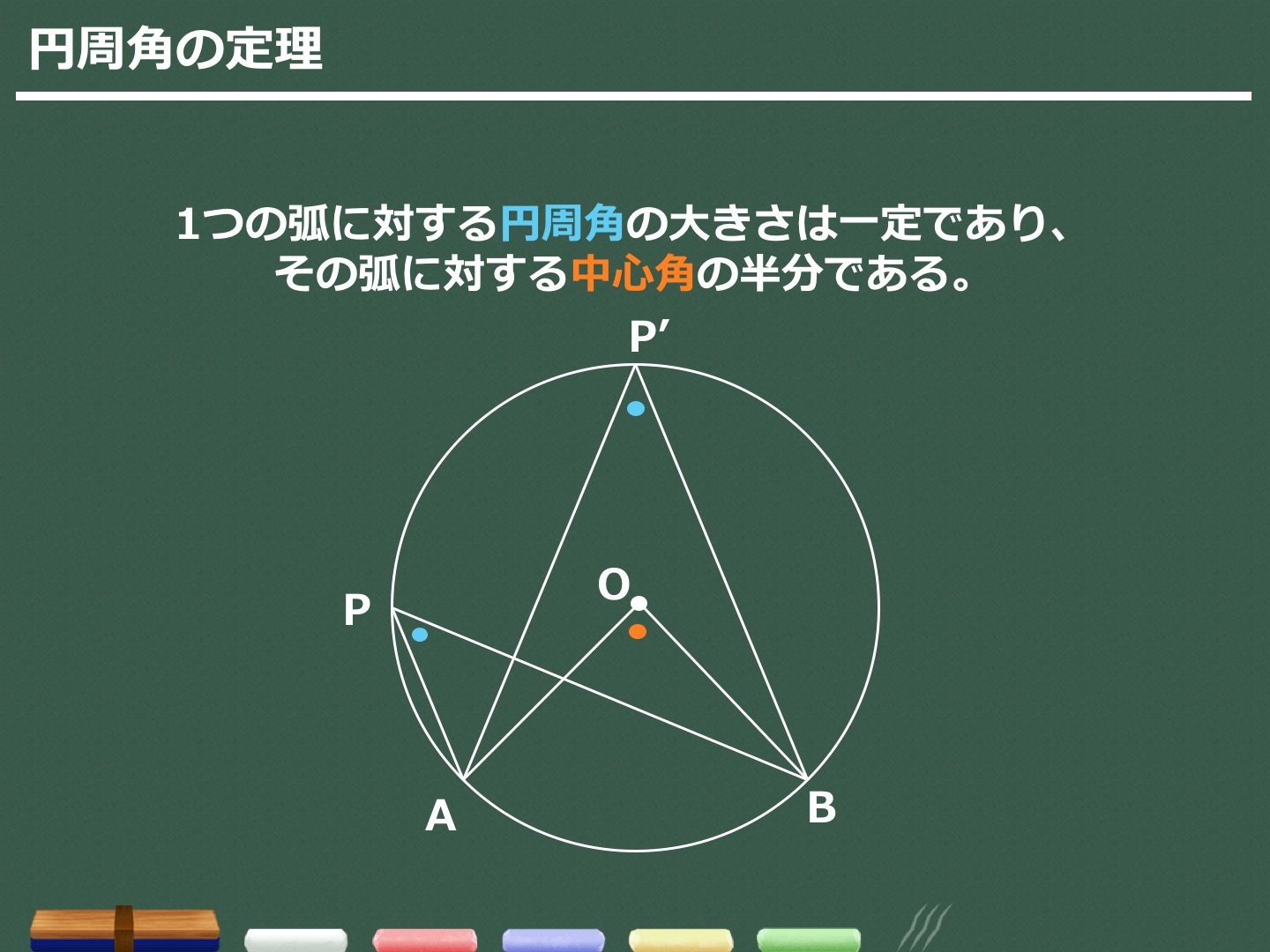
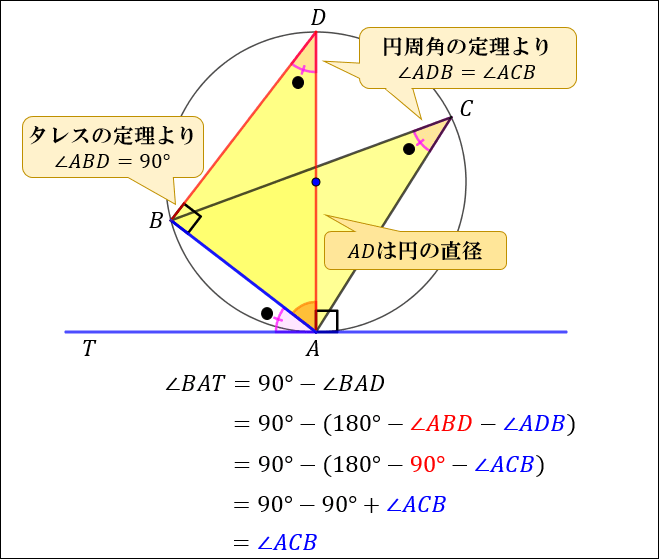
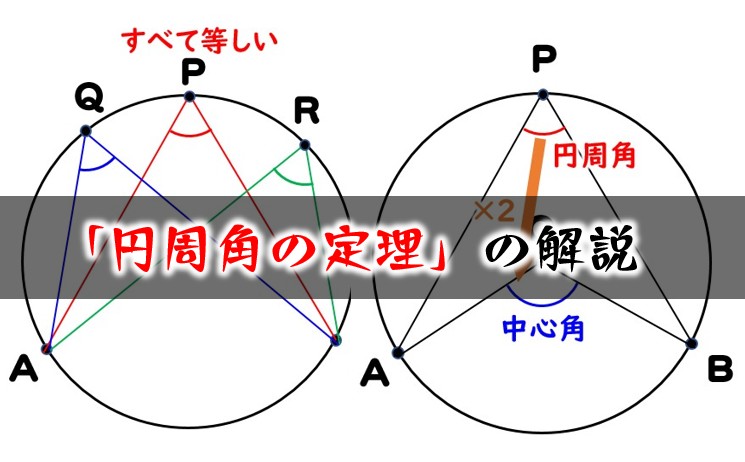
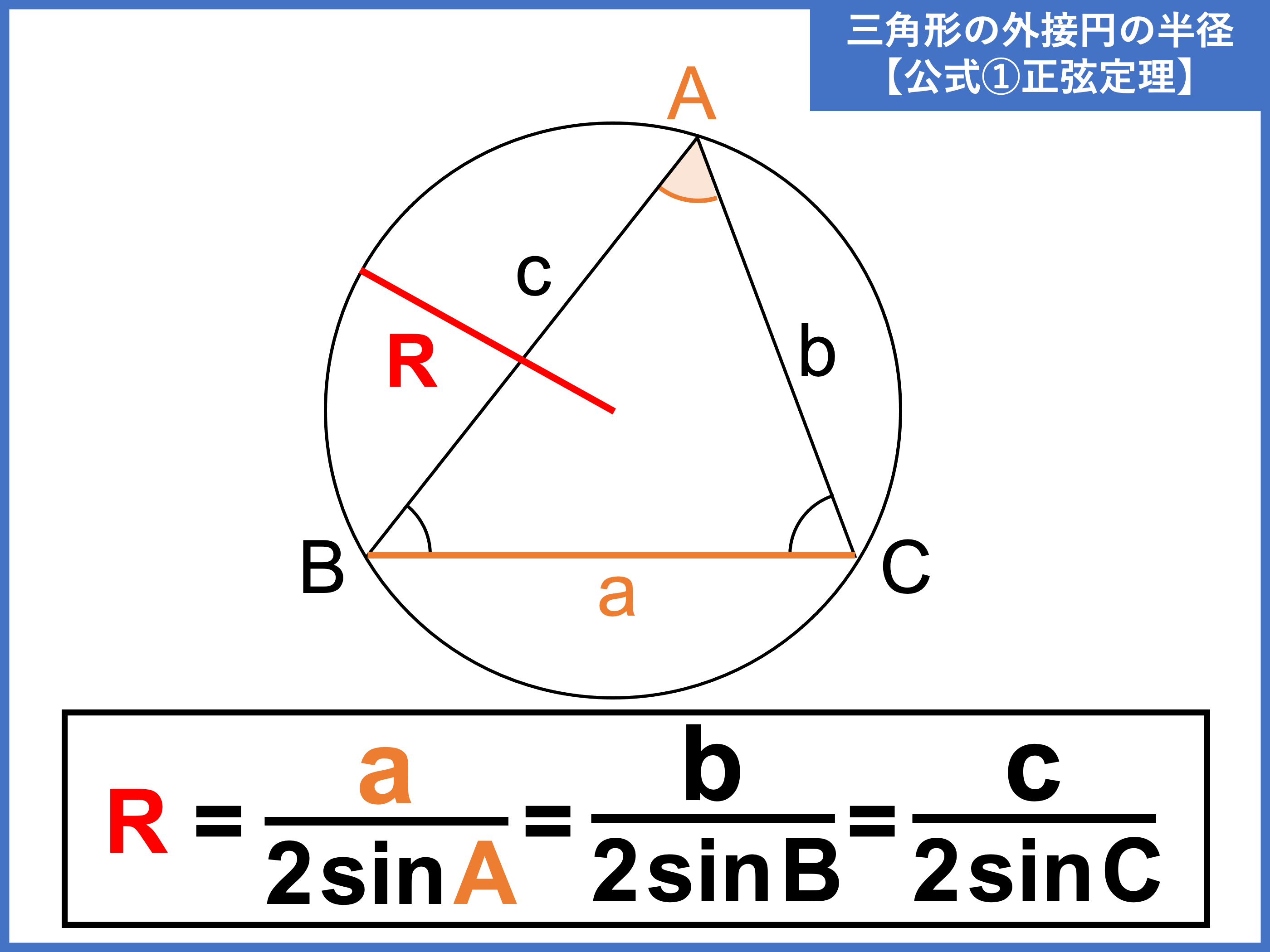
Web定理 円周上にある3点 A,B,C A,B,C を頂点とする三角形 ABC ABC について,1辺が円の直径と一致するなら, ABC ABC は直角三角形。 円周角の定理を用いて簡単に証明できます。 証明
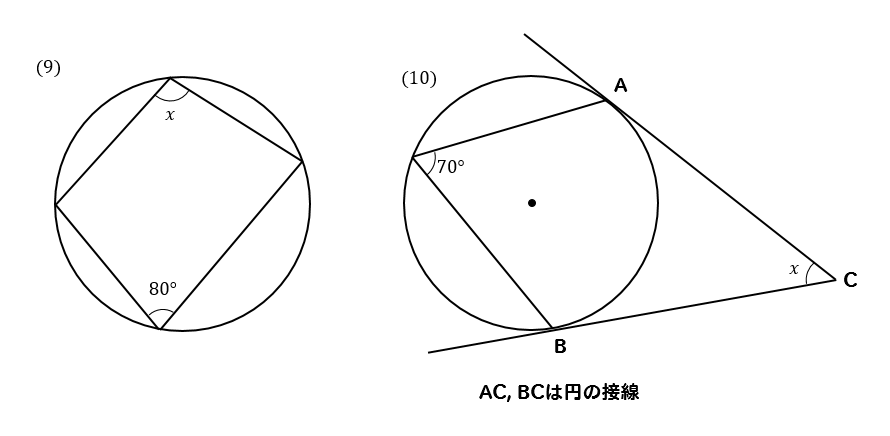
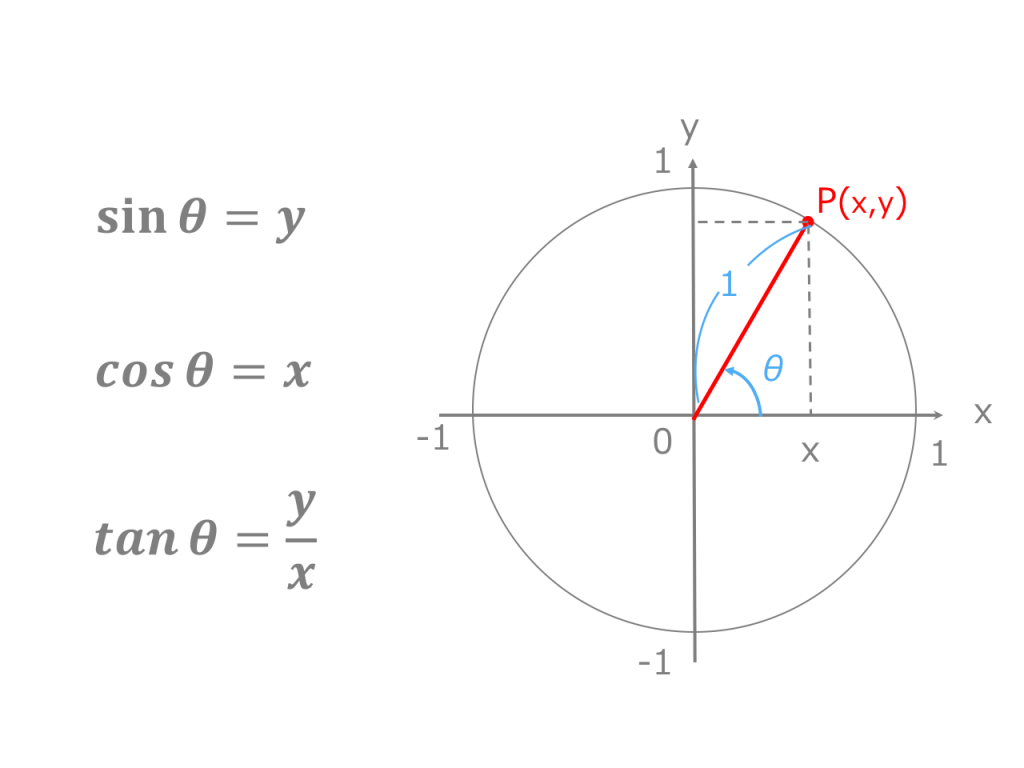
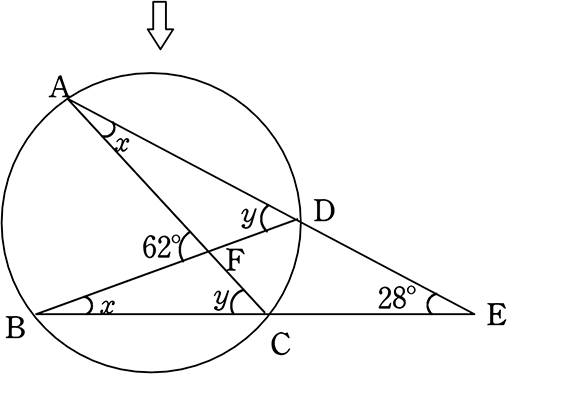
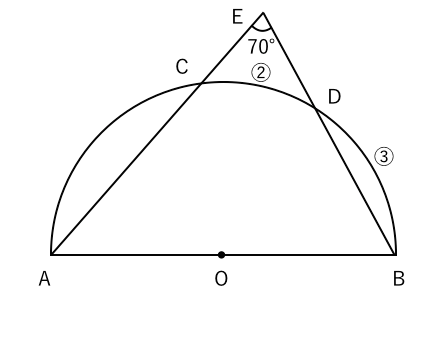
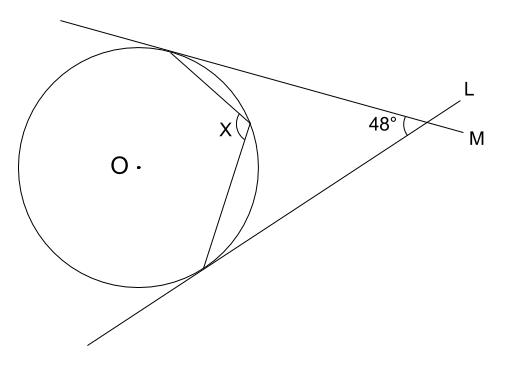
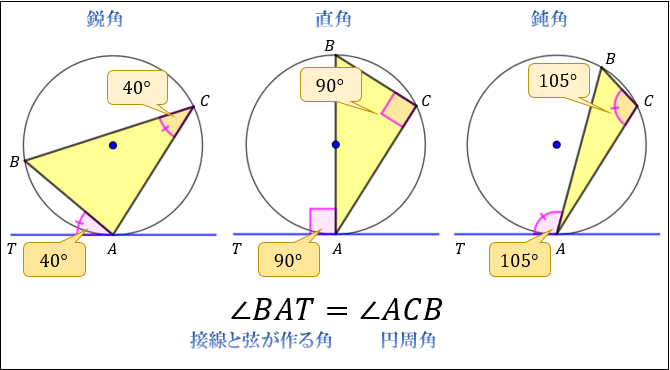
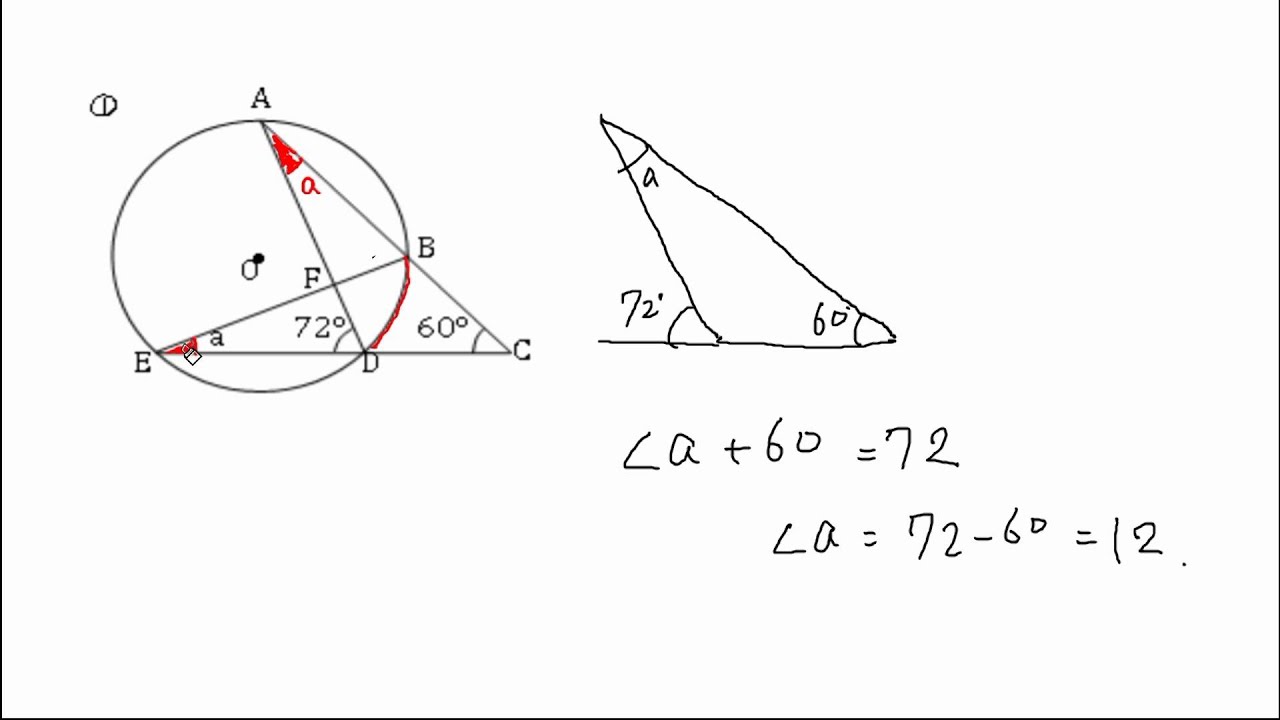
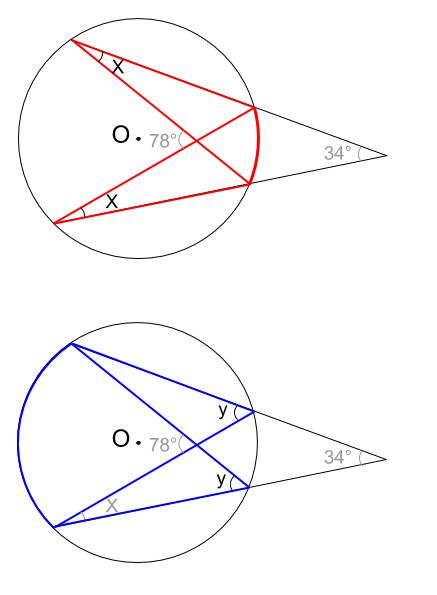
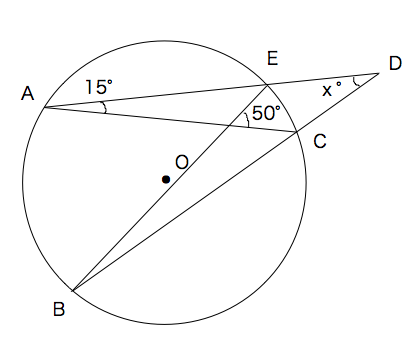
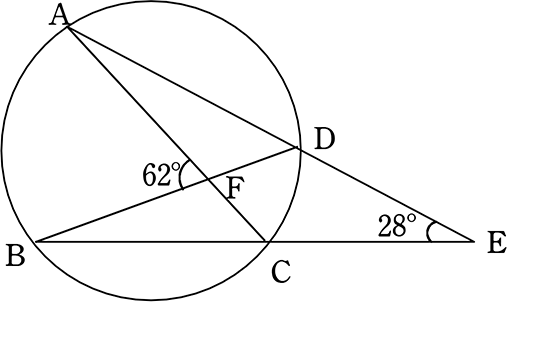
円 角度 求め方-Web円の外部の点 a から円 o に2つの接線が描ける。この接点を s, t とすると、線分 as, at の長さを接線の長さという。接線の長さは等しい。円の接線とその接点を通る弦が作る角は、その角WebAF ⌢ に対する円周角 ∠ A B F = 60 ° ÷ 2 = 30 ° BE ⌢ (青色) に対する円周角 ∠ B A E = 180 ° ÷ 2 = 90 ° 三角形の内角の和は 180 ° なので、 30 ° 90 ° x = 180 ° よって、 x = 60 ° (10)
円 角度 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 | ||
 | ||
「円 角度 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  |  |
「円 角度 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | ||
「円 角度 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 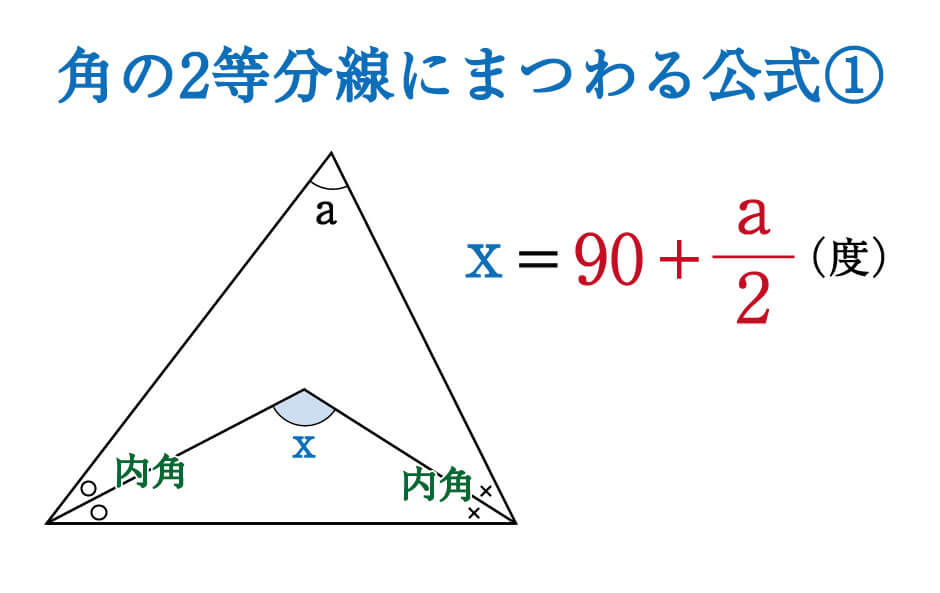 | 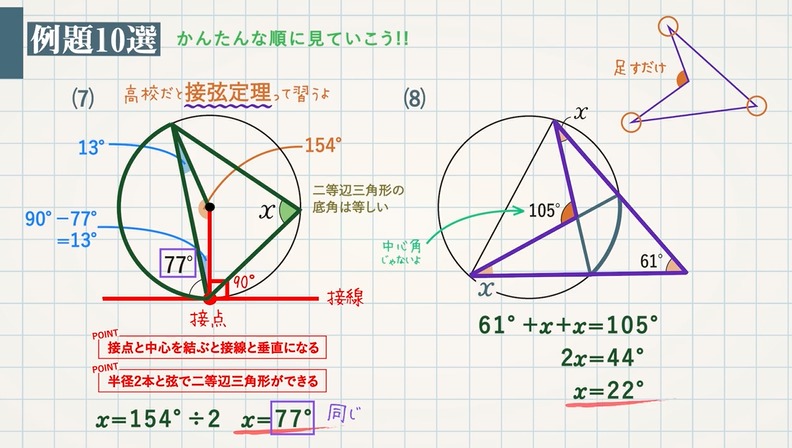 |
 | ||
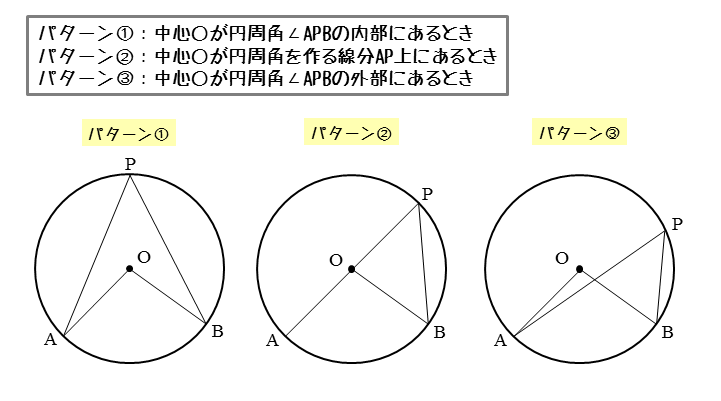 |  |  |
 | 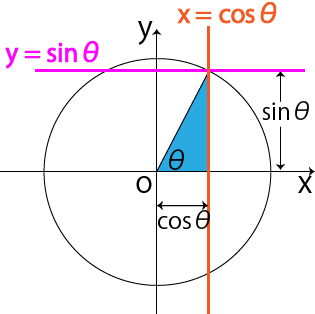 |  |
「円 角度 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「円 角度 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「円 角度 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  | |
「円 角度 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「円 角度 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 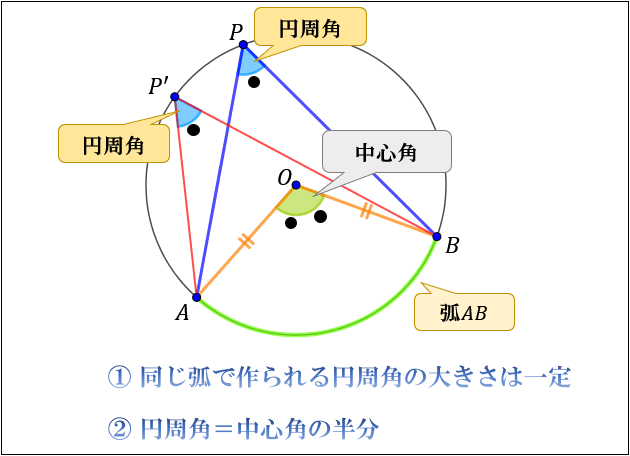 |
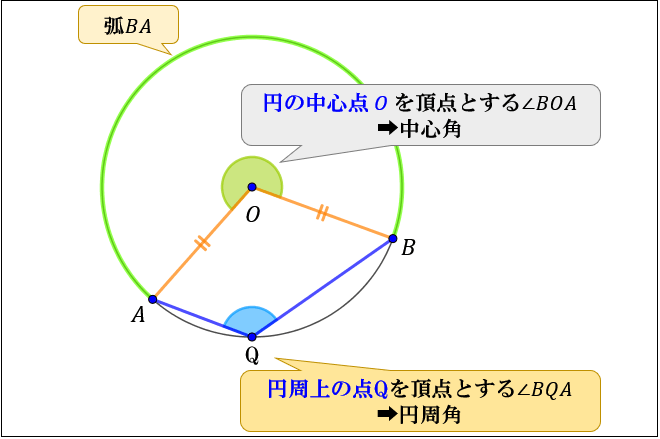
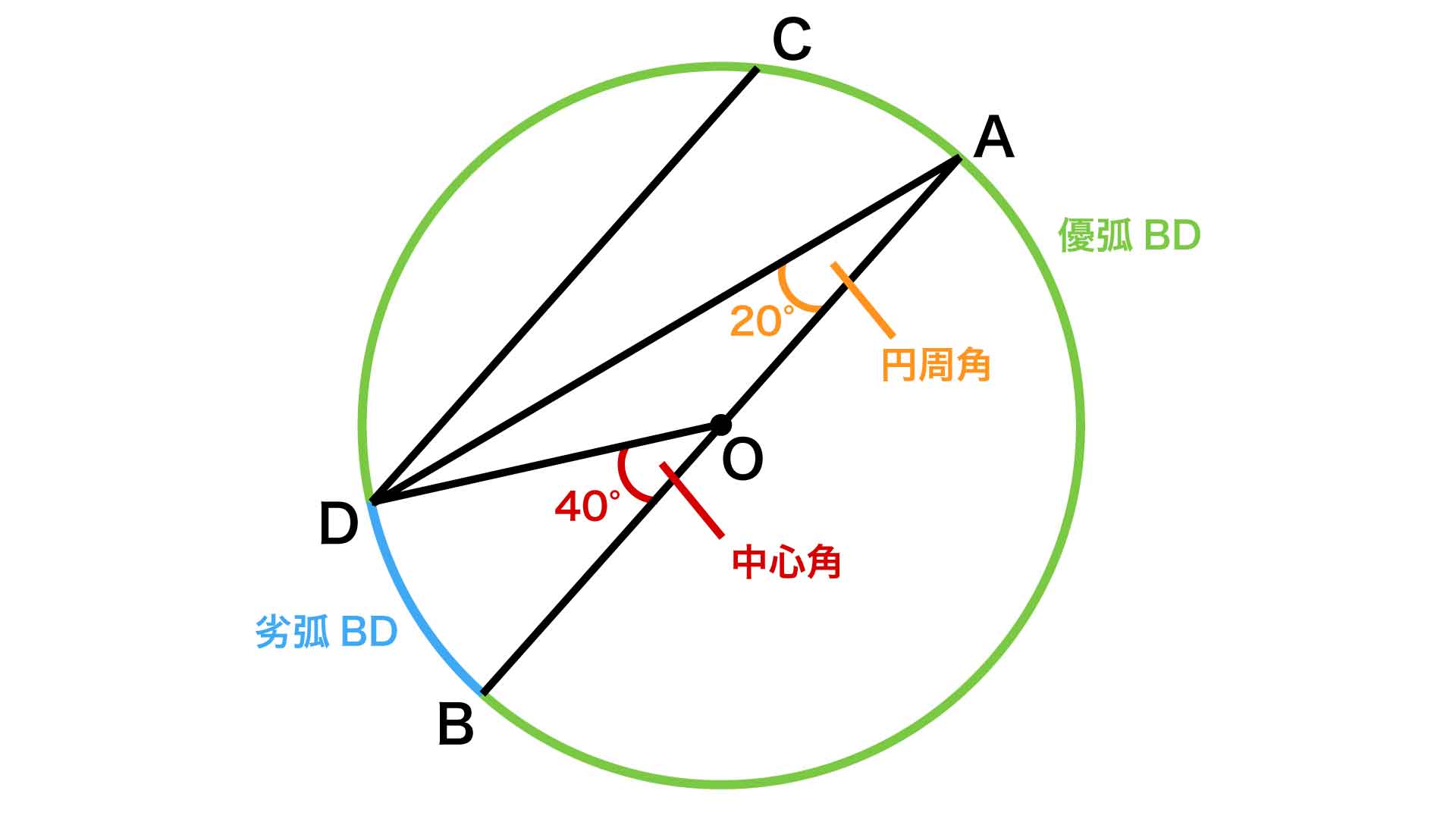
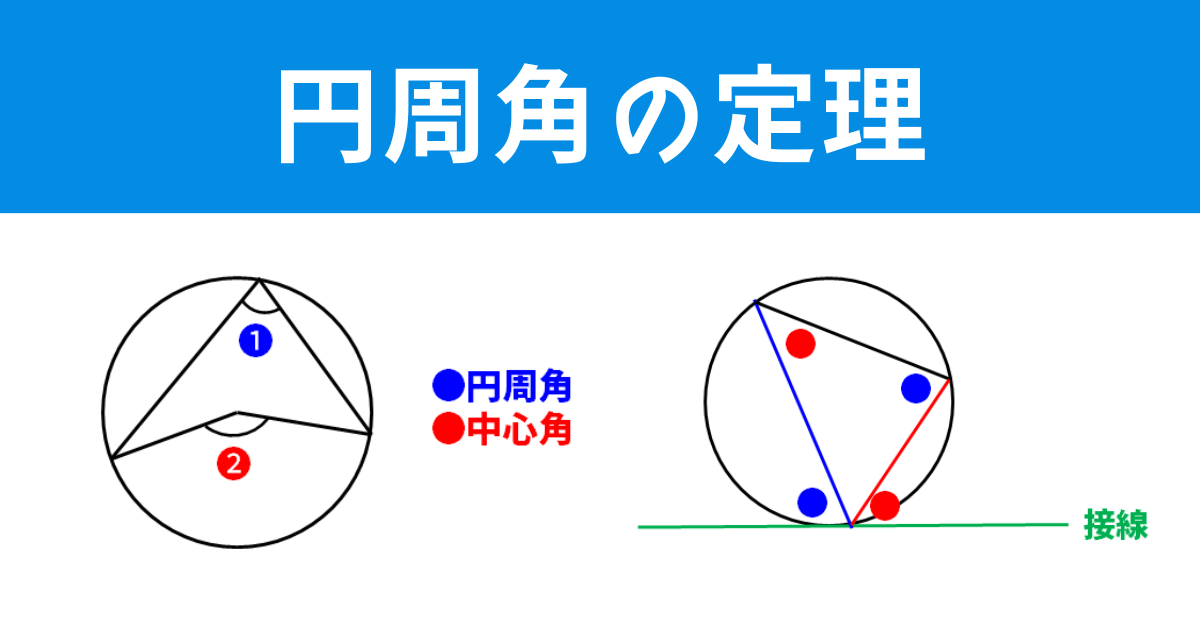
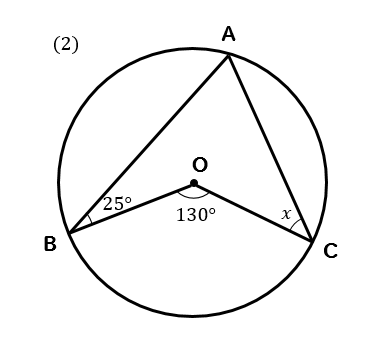
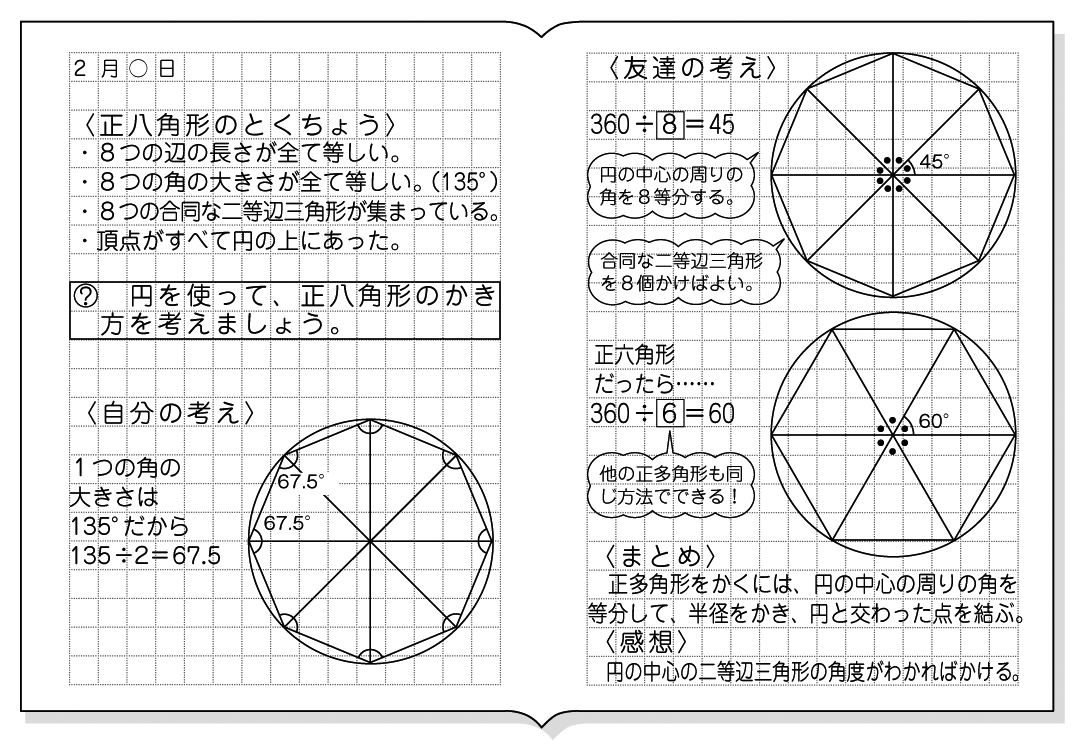
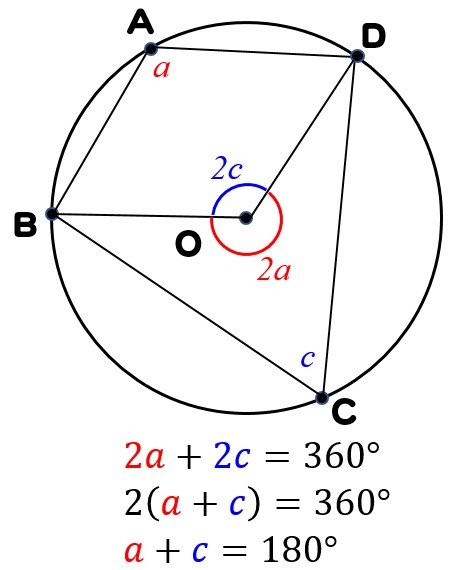
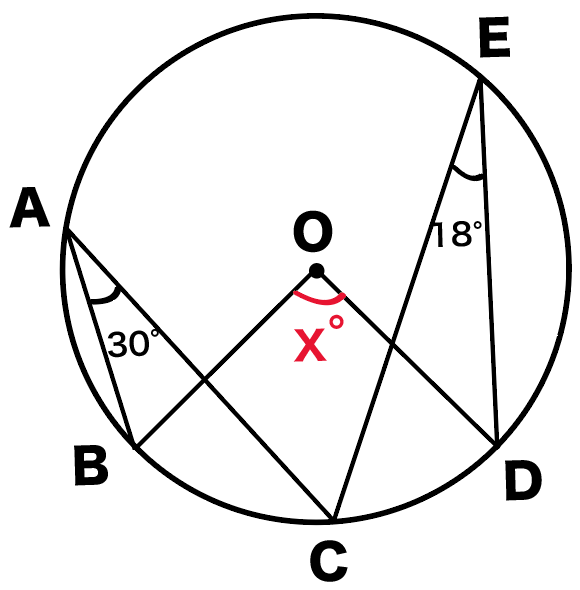
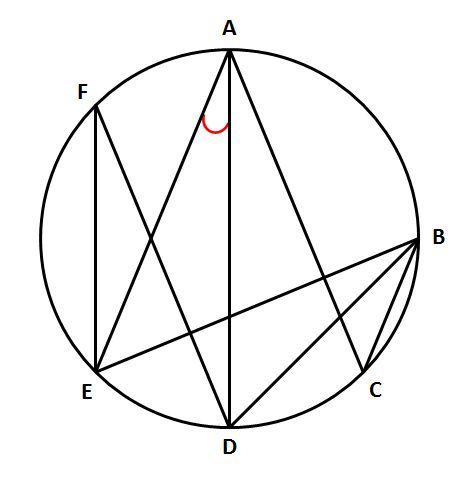
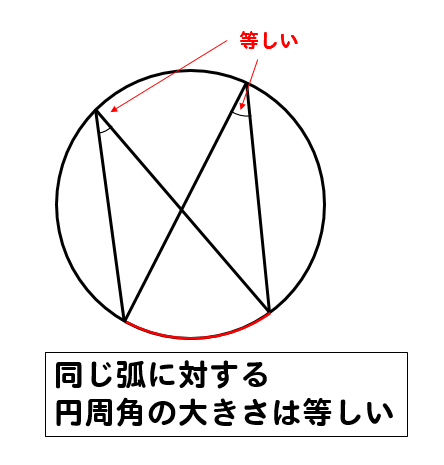
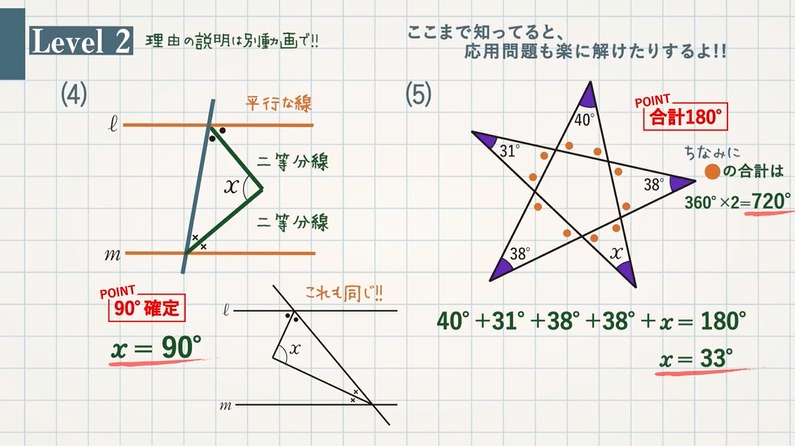
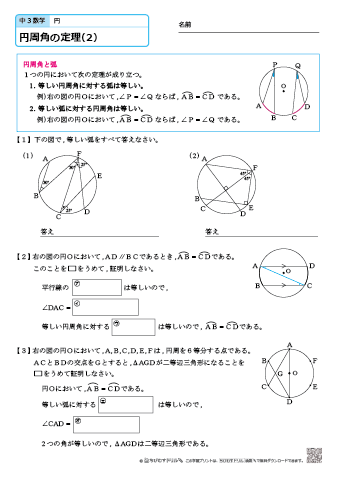
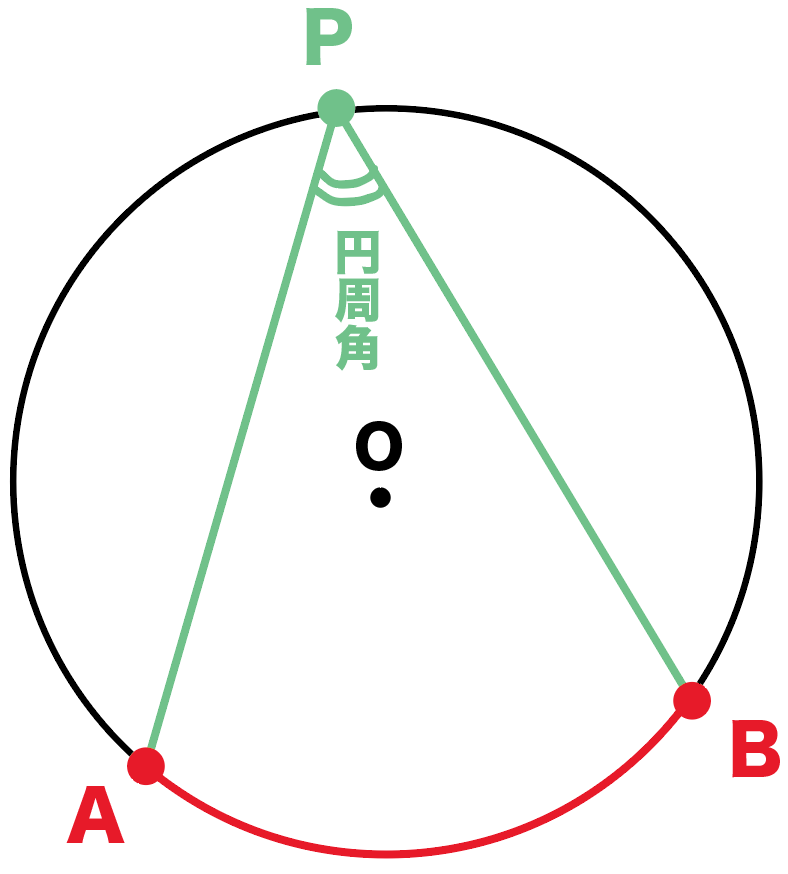
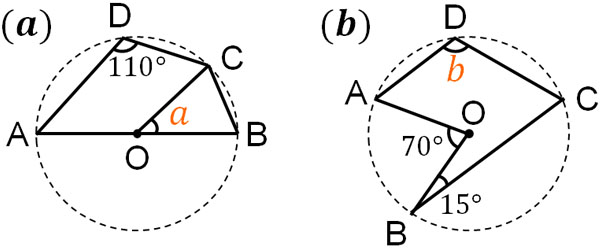
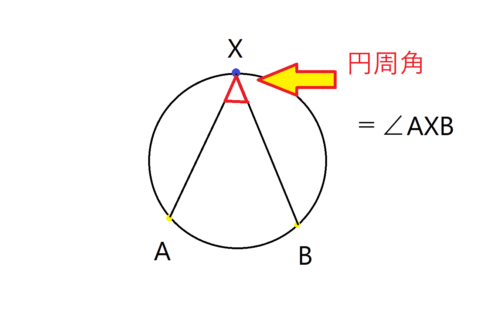
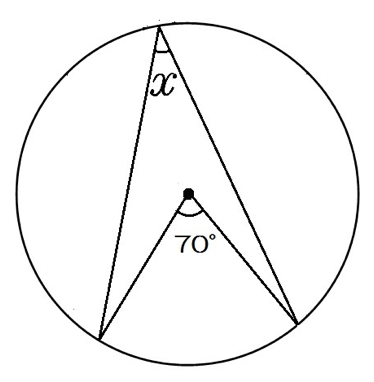
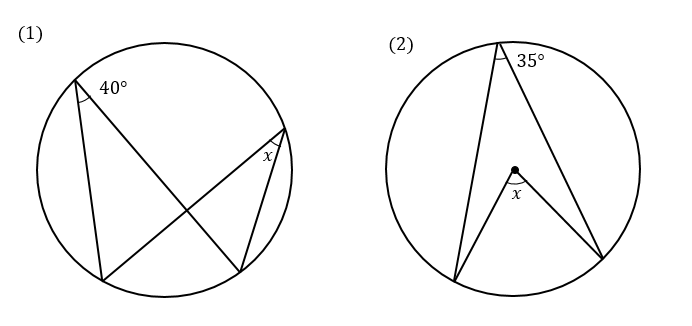
Web中心角の半分が必ず円周角になる 円周角の定理では中心角が頻繁に利用されます。 この理由として、円周角と中心角は以下の関係があるからです。 円周角 × 2 = 中心角 例えば円周角Web円周を8等分した点です x, y, z の角度を求めましょう →1コマあたりの中心角は 360°÷8 = 45° xは3コマ分の中心角の半分 (=円周角) → x = 1 2 1 2 (3×45°) = 135° 2 135 ° 2 = 675° 同様
Incoming Term: 円 角度 求め方,




0 件のコメント:
コメントを投稿